We have seen in this post about the concept of pressure that a solid exerts on a surface.
Today we are going to look at the pressure that a liquid exerts on the bottom of a container in which it is present.
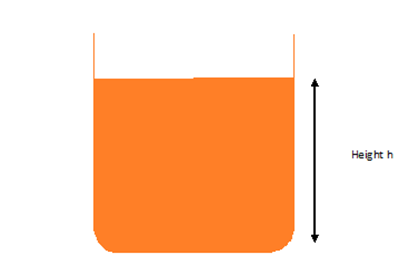
Fig 1 below shows a container containing an unknown orange liquid. The depth of liquid in the container is h. The density of the liquid is denoted by the letter ρ.
Fig 1
Fig 2 below represent the same container but this time in 3 dimensions. The container is in the form of a cuboid. The liquid will thus be in the form of a cuboid with cross-sectional area and height h.
Fig 2
Now how do you obtain the pressure that the liquid is exerting on the bottom of the container?
The equation for pressure is
Pressure = Force Applied /Surface area
= Force applied by liquid/surface area over which pressure is applied
= Weight of liquid /Cross-sectional area A
= mg /A
= (Volume of liquid *density*g)/A
= (Ah *ρ)*g/A
= h*ρ*g
= hρg
Where g is the acceleration due to gravity.
Example
A bottle of water of density 1000 kg/m3 has water of depth 0.10 m in it. If the acceleration due to gravity,g, is 9.81 m/s2 , calculate the pressure due to the water on the bottom of the container.
Pressure due to water =hρg
= 0.10*9.81*1000
=981 Pascal (Pa)


No comments:
Post a Comment