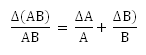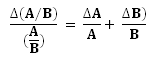As we have seen in earlier post an object can have either gravitational potential energy or kinetic energy. However it is always possible for the object to have both kinetic energy and gravitational potential energy. Think of a plane flying at a certain height above the ground.
It is going to have kinetic energy due to its speed and gravitational potential energy due to its height.
Now what happens to a body that is either falling toward the ground or rising to a certain height.
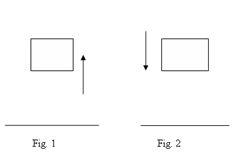
As you can see in fig 1 the object is rising and as a result its height is also rising, hence its potential energy is also increasing. Its kinetic energy is however decreasing. (see Principle of conservation of energy).
However the object in fig 2 is falling towards the ground. Since its height is decreasing, its gravitational potential energy must also be decreasing and its kinetic energy increasing.
Example 1
In this example a ball is released from rest from a height h.
If the ball is initially at rest then
v = 0 ms-1 hence Ek = 0 J
However since the object is at a height h the Ep = mgh
When the ball is released it fall under the effect of the force of gravity, as a result it will accelerate downward and as a result the velocity of the object will increase while the height of the object decreases.
Hence as the velocity decreases the kinetic energy decreases while the gravitational potential energy decreases as the height decreases.
However at all time Ek + Ep = Total energy and total energy is constant.
As the object reaches the ground the height becomes zero so does the gravitational potential energy while the kinetic energy reaches its maximum value. At this point all the gravitational potential energy would have been converted to kinetic energy.
When it reaches the ground h = 0 m hence Ep = 0 J
While Ek = 0.5 mv2
Example 1
A man of mass 64 kg jumps from a bridge 25 m high into a river.
(a) Calculate the gravitational potential energy of the man when he is on the bridge.
(b) What is his speed of entry into the water.
Now the man is on the bridge at a height of 25 m. It means that he has gravitational potential energy.
(a) Gravitational potential energy Ep = mgh
= 64*9.81*25
= 15696J
= 1.5 *104J
(b) When the person jumps the gravitational potential energy decreases as his height decreases. However as the person fall to the ground his speed increases and as a result the kinetic energy is completely converted to kinetic energy.
Hence what he reaches the river all the gravitational potential energy has been converted to kinetic energy.
Kinetic energy at surface of river = 1.5 *104J
Ek = 0.5 mv2
1.5 *104= 0.5 *64*v2
v = (1.5 *104/0.5/64)0.5
= 21.65 m s-1
=22 m s-1
It is now time for a question. I will give you an answer to do. I will give the answer when some of you have given the answers.
Good luck.
A girl of mass 50 kg is trying to jump over a bar. She ran at a speed of and leaves the ground and successfully jumped over the bar.
(a) Calculate the kinetic energy that she has when she is running.
(b) Deduce the gravitational potential energy of the girl when she is at her maximum height.
(c) Calculate the height of the bar.