In many questions in Physics or often in a practical students are often required to draw a line of best fit.
So what is the line of best fit. The line of best fit is a line that is drawn through a series of points in a graph in order to determine the trend in the points. The line can then be used to determine the gradient and the y-intercept of the line if it is a straight line.
The following are tips that you can use in order to obtain the best line of best fit from a few points. You should read all of them and choose which tips is appropriate.
Tip 1
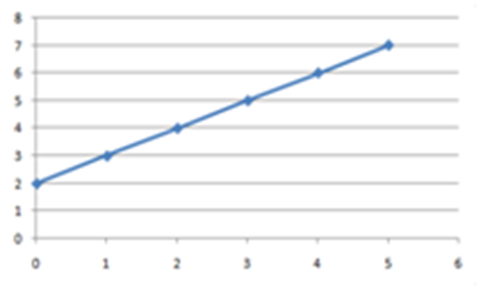
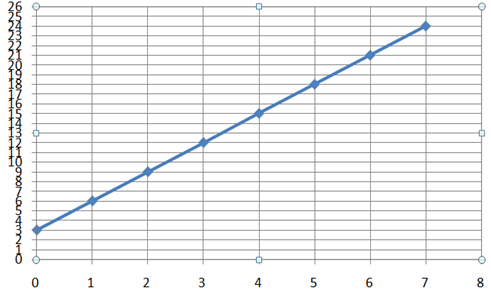
Sometimes you will obtains points that are as shown below in fig 1. Although I must say that such occurrence is quite rare. In fig 1 below you can see that the points forms an almost perfect straight line. In such a case it would be enough to choose two points far away from each other and then draw a line from one to the the other. Make sure that the line extends on both side to cover all the points.
Fig 1
Tip 2
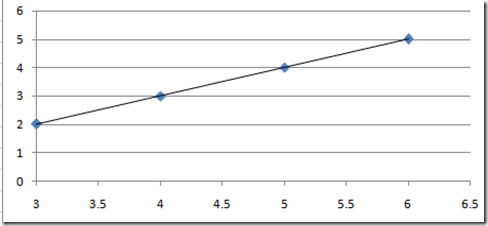
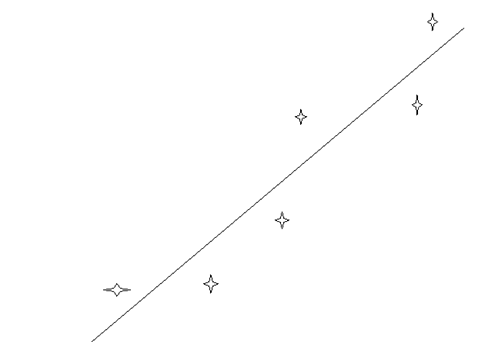
Most of the time you will be faced with points as in fig 2 below. As such you will have to draw a line such that the points are on both sides of the lines as such. A you see from one side of the line to the other the points alternates up and down. Also make sure that two points that are closest to each other and are on different sides of the line are the same distance from the line.
Fig 2
Tip 3
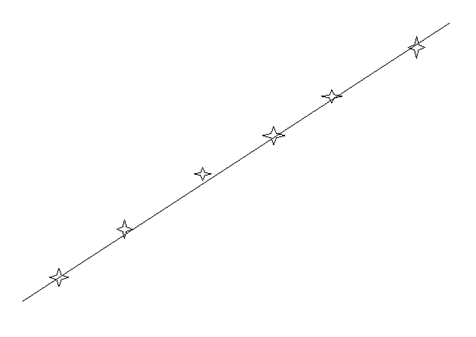
In case you are unable to make the points alternate on both sides of the line from one end of the line to the other as in fig 3 below. It is acceptable to have them two by two on the same side of the line.
Fig 3
Tip 4
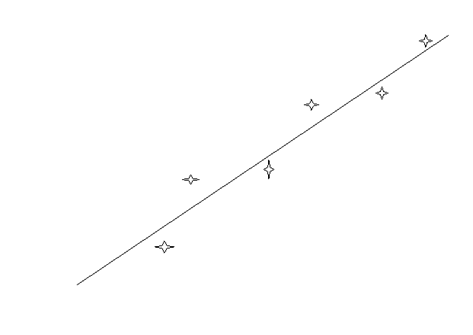
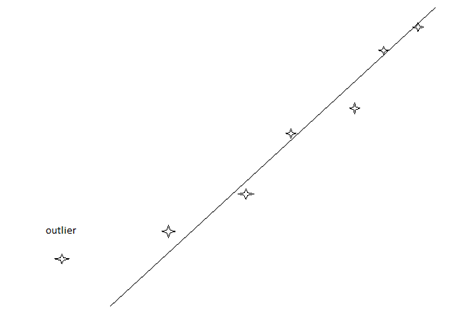
It may happen as in fig 4 below that one point is so far from the others that it would make no sense to include it when drawing the line of best fit. This point is called an outlier and it is often the result of an error in calculation, an error in taking readings such as parallax error or zero error. It is advisable to check the data again.
Fig 4
Tip 5
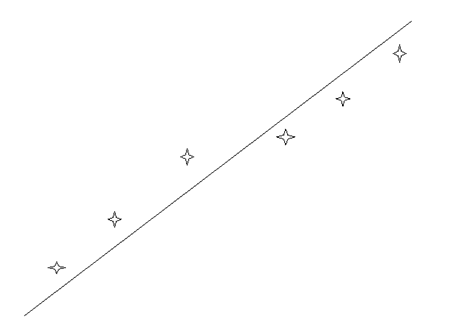
Although I had said that it is possible to have the points two by two on both side of the line. It is not possible to have them as in fig 5 below.
Fig 5
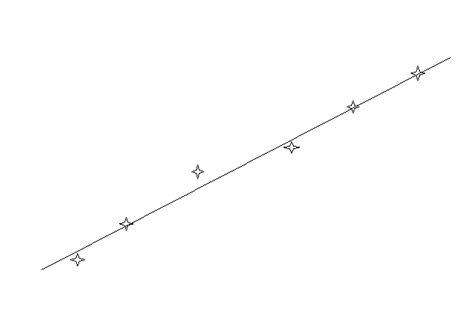
If you are in the situation that I described as in fig 5 above then you can draw the line as in the fig 6 below.
Fig 6
So if you have any difficulties drawing the line then review the five different tips above you will surely find a tip for you. Otherwise send me a picture of the points and we will see it together.

![clip_image001[14] clip_image001[14]](http://lh6.ggpht.com/_MLcxcpYx4ws/TNUV9HwUoPI/AAAAAAAAAjM/YhKIYzQC7Dk/clip_image00114_thumb2.gif?imgmax=800)
![clip_image001[16] clip_image001[16]](http://lh6.ggpht.com/_MLcxcpYx4ws/TNUWOf_bKwI/AAAAAAAAAjU/AcloNLWGMvQ/clip_image00116_thumb2.gif?imgmax=800)