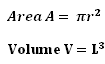Distance and displacement are two quantities that are used to describe motion. We are going to have a look at both of them and see how to differentiate between the two.
Distance
Distance is a scalar quantity and the SI unit is the Metre (m)
Example 1
![clip_image001[11] clip_image001[11]](http://lh3.ggpht.com/_MLcxcpYx4ws/SwzHtACOGGI/AAAAAAAAAJY/H2J8uNd4Fmk/clip_image00111_thumb1.gif?imgmax=800)
Now suppose a person moves from an initial position of A and travels to a final position of B. The line connecting the two points is the path that the person would take. Now the distance travelled is the length of the path taken by the person from the initial position to the final position.
Example 2
![clip_image001[9] clip_image001[9]](http://lh3.ggpht.com/_MLcxcpYx4ws/SwzH3RRNQaI/AAAAAAAAAJg/C6TkOn01uFw/clip_image0019_thumb1.gif?imgmax=800)
Now if the path is not a straight line like in the diagram shown above then the distance travelled is the length of the path from A to B through all the turns as measured with a measuring tape.
Example 3
![clip_image001[19] clip_image001[19]](http://lh5.ggpht.com/_MLcxcpYx4ws/SwzIBvs6HRI/AAAAAAAAAJo/FFg0I8L1X0A/clip_image00119_thumb1.gif?imgmax=800)
The next example is shown above. The person moves from A to D. The path is a line moving from A to B to C and then finally to D. Then the distance travelled is the length of the path AB+ the length of the path BC + the length of the path CD
Displacement
Displacement is a vector quantity and the SI unit is the metre (m)
The displacement is a vector representing the shortest path from the initial position to the final position. It is thus a vector quantity. Let us have a look at the different motion above and see how the displacement is determined and how it is different from the distance.
Example 4
As we have seen in example 1 above the person moves from the initial position A to the final position B.
![clip_image001[21] clip_image001[21]](http://lh3.ggpht.com/_MLcxcpYx4ws/SwzIIQ4le4I/AAAAAAAAAJw/b5N72FX9PqM/clip_image00121_thumb.gif?imgmax=800)
As you can see the person moves from the initial position A to the final position B and the vector representing this motion is as shown. And the displacement is represented by this vector. Hence the displacement will have both a magnitude which would be the length of the vector and a direction which would be the direction of the vector.
For example 4 above we can say that the displacement is 10 m to the east.
Displacement = 10 m to the east
or Displacement = 10 m to the right
As you can see the displacement would have both a magnitude and a direction since it is a vector quantity.
Example 5
![clip_image001[25] clip_image001[25]](http://lh4.ggpht.com/_MLcxcpYx4ws/SwzIPur9xeI/AAAAAAAAAJ4/1cMUr3_f-gQ/clip_image00125_thumb2.gif?imgmax=800)
This is the same motion that we used in example 2. The person moves from the initial position A and travels until he reaches the final position B. As you can see on the diagram above there is a vector from the initial position A to the final position B. This vector represent the displacement of the person where the length of the vector is its magnitude and the direction of the vector the direction of the displacement.
In this case the displacement of the person can be said to be
Displacement = 10 m 15o clockwise from the horizontal,
Where the line AC represent the easterly direction,
Example 6
Now let us look at the same motion example that the person did in example 3. The person walks from A to B to C and finally arrives at D. You can see on the diagram below that I have drawn a vector AD that starts from the point A and ends at the point D. This vector is the displacement vector and as you can see it has a magnitude and a direction.
We can say for example that the displacement is as shown
Displacement = 15 m 150 clockwise from the horizontal
![clip_image001[6] clip_image001[6]](http://lh4.ggpht.com/_MLcxcpYx4ws/SwzIZtjJqiI/AAAAAAAAAKA/JEbww2G8D4w/clip_image0016_thumb1.gif?imgmax=800)
As you have seen displacement and distance are two quantities easy to understand and to differentiate but as usual if you have any question you can leave them here and I would answer then as soon as possible.

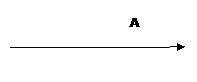
![clip_image001[6] clip_image001[6]](http://lh3.ggpht.com/_MLcxcpYx4ws/SwzVbpu89rI/AAAAAAAAAMc/uhZucW9ieh8/clip_image0016_thumb.gif?imgmax=800)
![clip_image001[8] clip_image001[8]](http://lh5.ggpht.com/_MLcxcpYx4ws/SwzVh4NRzsI/AAAAAAAAAMk/d_7N_as--rw/clip_image0018_thumb.gif?imgmax=800)
![clip_image001[10] clip_image001[10]](http://lh6.ggpht.com/_MLcxcpYx4ws/SwzVmSW8QfI/AAAAAAAAAMo/JsPW1b5-hvY/clip_image00110_thumb.gif?imgmax=800)
![clip_image001[12] clip_image001[12]](http://lh4.ggpht.com/_MLcxcpYx4ws/SwzVxtYlJDI/AAAAAAAAAMw/MrtX1sudUC0/clip_image00112_thumb.gif?imgmax=800)
![clip_image001[14] clip_image001[14]](http://lh5.ggpht.com/_MLcxcpYx4ws/SwzWA4dFKbI/AAAAAAAAAM4/wkDQb3JSgDA/clip_image00114_thumb.gif?imgmax=800)
![clip_image001[16] clip_image001[16]](http://lh5.ggpht.com/_MLcxcpYx4ws/SwzWLtqWA6I/AAAAAAAAANA/xGX6e9eRFBg/clip_image00116_thumb2.gif?imgmax=800)
![clip_image001[18] clip_image001[18]](http://lh6.ggpht.com/_MLcxcpYx4ws/SwzWdTUA91I/AAAAAAAAANI/ZLn6Hy5hqi0/clip_image00118_thumb1.gif?imgmax=800)
![clip_image001[22] clip_image001[22]](http://lh4.ggpht.com/_MLcxcpYx4ws/SwzWl6OUg3I/AAAAAAAAANQ/RcilPB2mIPA/clip_image00122_thumb2.gif?imgmax=800)
![clip_image001[28] clip_image001[28]](http://lh5.ggpht.com/_MLcxcpYx4ws/SwzWusmmELI/AAAAAAAAANY/wUS_zW6ki9w/clip_image00128_thumb1.gif?imgmax=800)

![clip_image001[5] clip_image001[5]](http://lh3.ggpht.com/_MLcxcpYx4ws/SwzM_RDtADI/AAAAAAAAAK8/zkr9vP4q2vs/clip_image0015_thumb1.gif?imgmax=800)
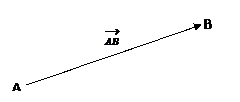
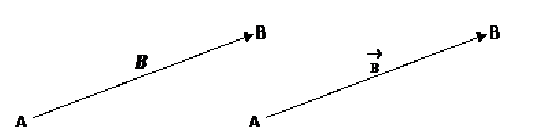
![clip_image001[7] clip_image001[7]](http://lh4.ggpht.com/_MLcxcpYx4ws/SwzOAnQRJPI/AAAAAAAAALk/vb2oOEnMBUs/clip_image0017_thumb.gif?imgmax=800)
![clip_image001[17] clip_image001[17]](http://lh4.ggpht.com/_MLcxcpYx4ws/SwzOLCxnHiI/AAAAAAAAALs/3fkkIZzFJT0/clip_image00117_thumb.gif?imgmax=800)
![clip_image001[19] clip_image001[19]](http://lh6.ggpht.com/_MLcxcpYx4ws/SwzOSqhni5I/AAAAAAAAAL0/nBSt4EAoHHg/clip_image00119_thumb.gif?imgmax=800)
![clip_image001[21] clip_image001[21]](http://lh5.ggpht.com/_MLcxcpYx4ws/SwzTsqvW07I/AAAAAAAAAL8/FFBYC3GrvRk/clip_image00121_thumb.gif?imgmax=800)
![clip_image001[5] clip_image001[5]](http://lh5.ggpht.com/_MLcxcpYx4ws/SwzT3_MVOSI/AAAAAAAAAME/wNMchPflnTM/clip_image0015_thumb2.gif?imgmax=800)
![clip_image001[25] clip_image001[25]](http://lh6.ggpht.com/_MLcxcpYx4ws/SwzUAm7rjtI/AAAAAAAAAMM/sYtquuJ587M/clip_image00125_thumb1.gif?imgmax=800)


![clip_image001[11] clip_image001[11]](http://lh3.ggpht.com/_MLcxcpYx4ws/SwzHtACOGGI/AAAAAAAAAJY/H2J8uNd4Fmk/clip_image00111_thumb1.gif?imgmax=800)
![clip_image001[9] clip_image001[9]](http://lh3.ggpht.com/_MLcxcpYx4ws/SwzH3RRNQaI/AAAAAAAAAJg/C6TkOn01uFw/clip_image0019_thumb1.gif?imgmax=800)
![clip_image001[19] clip_image001[19]](http://lh5.ggpht.com/_MLcxcpYx4ws/SwzIBvs6HRI/AAAAAAAAAJo/FFg0I8L1X0A/clip_image00119_thumb1.gif?imgmax=800)
![clip_image001[21] clip_image001[21]](http://lh3.ggpht.com/_MLcxcpYx4ws/SwzIIQ4le4I/AAAAAAAAAJw/b5N72FX9PqM/clip_image00121_thumb.gif?imgmax=800)
![clip_image001[25] clip_image001[25]](http://lh4.ggpht.com/_MLcxcpYx4ws/SwzIPur9xeI/AAAAAAAAAJ4/1cMUr3_f-gQ/clip_image00125_thumb2.gif?imgmax=800)
![clip_image001[6] clip_image001[6]](http://lh4.ggpht.com/_MLcxcpYx4ws/SwzIZtjJqiI/AAAAAAAAAKA/JEbww2G8D4w/clip_image0016_thumb1.gif?imgmax=800)