Parallax error is the error that is most committed when readings are taken in physics. You can thus understand why it is important to avoid it at all cost. One must be aware of its existence at all time so that it can be avoided and as a result the true value of the reading is obtained.
The concept of parallax error is related to the term parallax.
Imagine that we have in a room a pelican and a flamingo as shown in fig 1 below.
Fig 1
Now Garfield is moving about in the room and each time is is somewhere in the room, he looks at the two birds. At the point A he sees the flamingo on the left of the pelican whereas when he is at position C he would see the flamingo on the right of the pelican. Only when he would be at position B would he sees the two birds one behind the other.
He would discover that each time he is at a different position, he would find that the position of the flamingo relative to the pelican has changed.
You can also have this effect when you are in front of a clock. If you move from side to side you would find that the time that you can read from the clock is different.
So we can the understand that the parallax is the change in the apparent position of an object when the position of the observer changes.
Now let us look at the concept of parallax error. If you have placed a pencil on a metre rule and you are reading its length then just like in fig 1 above and in fig 2 below you can place you eye everywhere you want.
Fig 2
As you can see from fig 2 above I have chosen three position at which you can place your eye.
Clearly at these three position we can have the following reading
Reading at A = 6.2 cm
Reading at B = 5.8 cm
Reading at C = 5.5 cm
What you you think would be the correct reading?
The correct reading is would be obtained when the eye is placed at B.
Fig 3
Now there is a line from the tip of eye to the of the pencil that continues up to the scale. this line is called the line of sight and the mark at which the line intersect the scale is the length of the pencil. This line of sight must be be at right angle to the scale. This is shown above in fig
If the line of sight and the scale are not ar right angle to each other then a parallax error is committed.
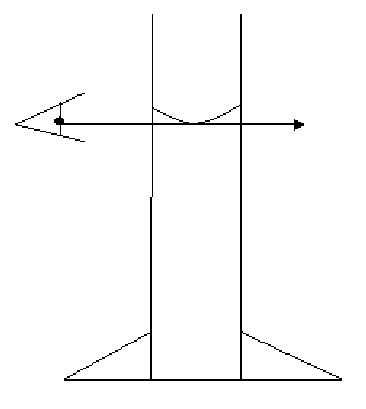
Similarly with a measuring cylinder the line of sight from the eye to the bottom of the meniscus must be at right angle to the scale as shown in fig 4 below. In this case the line of sight is horizontal and the scale vertical.
Fig 4
So as you can see above each time you are taking a reading you must ensure that the line of sight is perpendicular to the scale.

![clip_image004[10] clip_image004[10]](http://lh5.ggpht.com/_MLcxcpYx4ws/SzGUePOvPyI/AAAAAAAAAQ4/8JYZbH7-GVA/clip_image00410_thumb2.gif?imgmax=800)
![clip_image002[13] clip_image002[13]](http://lh3.ggpht.com/_MLcxcpYx4ws/SzGVMDClCrI/AAAAAAAAARA/3dGdBJwo_90/clip_image00213_thumb2.gif?imgmax=800)
![clip_image002[15] clip_image002[15]](http://lh3.ggpht.com/_MLcxcpYx4ws/SzGVlrK7VLI/AAAAAAAAARI/r6JXK9GcBr0/clip_image00215_thumb1.gif?imgmax=800)
![clip_image001[3] clip_image001[3]](http://lh3.ggpht.com/_MLcxcpYx4ws/SzGP8Qm4u6I/AAAAAAAAAQA/qZ2mIgtsfl4/clip_image0013_thumb.gif?imgmax=800)
![clip_image001[5] clip_image001[5]](http://lh6.ggpht.com/_MLcxcpYx4ws/SzGQMnCSWgI/AAAAAAAAAQI/ghB5j6pKw4k/clip_image0015_thumb.gif?imgmax=800)
![clip_image001[9] clip_image001[9]](http://lh4.ggpht.com/_MLcxcpYx4ws/SzGQauJ827I/AAAAAAAAAQQ/Wc5ev4i7YXc/clip_image0019_thumb.gif?imgmax=800)
![clip_image001[11] clip_image001[11]](http://lh3.ggpht.com/_MLcxcpYx4ws/SzGQpi9fbPI/AAAAAAAAAQY/3Owa_B5BTgY/clip_image00111_thumb.gif?imgmax=800)

![clip_image001[5] clip_image001[5]](http://lh6.ggpht.com/_MLcxcpYx4ws/SzGRJlPa-wI/AAAAAAAAAQo/XrMxUkuCz78/clip_image0015_thumb1.gif?imgmax=800)
![clip_image001[6] clip_image001[6]](http://lh3.ggpht.com/_MLcxcpYx4ws/SzGRYUiUrKI/AAAAAAAAAQw/l1MR57v36_Y/clip_image0016_thumb1.gif?imgmax=800)
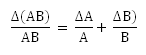
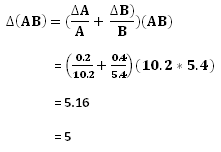
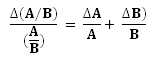
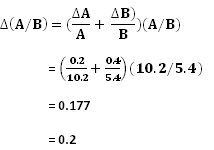

![clip_image001[10] clip_image001[10]](http://lh5.ggpht.com/_MLcxcpYx4ws/SyYVyntgu_I/AAAAAAAAAOs/J-VgwV_glHE/clip_image00110_thumb1.gif?imgmax=800)
![clip_image001[12] clip_image001[12]](http://lh5.ggpht.com/_MLcxcpYx4ws/SyYWAFz6KLI/AAAAAAAAAO0/1bBviPEjQDc/clip_image00112_thumb1.gif?imgmax=800)
![clip_image001[16] clip_image001[16]](http://lh6.ggpht.com/_MLcxcpYx4ws/SyYWJjApX1I/AAAAAAAAAO8/3ir8KRbFke4/clip_image00116_thumb1.gif?imgmax=800)
![clip_image001[18] clip_image001[18]](http://lh4.ggpht.com/_MLcxcpYx4ws/SyYWZ_Q6EhI/AAAAAAAAAPE/xmKOLTqZ7OY/clip_image00118_thumb2.gif?imgmax=800)
![clip_image001[5] clip_image001[5]](http://lh4.ggpht.com/_MLcxcpYx4ws/SyYTCQcUODI/AAAAAAAAANs/2bJwoK91GJs/clip_image0015_thumb1.gif?imgmax=800)
![clip_image001[7] clip_image001[7]](http://lh5.ggpht.com/_MLcxcpYx4ws/SyYTd03X_XI/AAAAAAAAAN8/Pfo83rSpbFU/clip_image0017_thumb1.gif?imgmax=800)
![clip_image001[9] clip_image001[9]](http://lh5.ggpht.com/_MLcxcpYx4ws/SyYTyC2-EII/AAAAAAAAAOE/3vffM7oWQvQ/clip_image0019_thumb2.gif?imgmax=800)
![clip_image001[6] clip_image001[6]](http://lh3.ggpht.com/_MLcxcpYx4ws/SwzVbpu89rI/AAAAAAAAAMc/uhZucW9ieh8/clip_image0016_thumb.gif?imgmax=800)
![clip_image001[8] clip_image001[8]](http://lh5.ggpht.com/_MLcxcpYx4ws/SwzVh4NRzsI/AAAAAAAAAMk/d_7N_as--rw/clip_image0018_thumb.gif?imgmax=800)
![clip_image001[10] clip_image001[10]](http://lh6.ggpht.com/_MLcxcpYx4ws/SwzVmSW8QfI/AAAAAAAAAMo/JsPW1b5-hvY/clip_image00110_thumb.gif?imgmax=800)
![clip_image001[12] clip_image001[12]](http://lh4.ggpht.com/_MLcxcpYx4ws/SwzVxtYlJDI/AAAAAAAAAMw/MrtX1sudUC0/clip_image00112_thumb.gif?imgmax=800)
![clip_image001[14] clip_image001[14]](http://lh5.ggpht.com/_MLcxcpYx4ws/SwzWA4dFKbI/AAAAAAAAAM4/wkDQb3JSgDA/clip_image00114_thumb.gif?imgmax=800)
![clip_image001[16] clip_image001[16]](http://lh5.ggpht.com/_MLcxcpYx4ws/SwzWLtqWA6I/AAAAAAAAANA/xGX6e9eRFBg/clip_image00116_thumb2.gif?imgmax=800)
![clip_image001[18] clip_image001[18]](http://lh6.ggpht.com/_MLcxcpYx4ws/SwzWdTUA91I/AAAAAAAAANI/ZLn6Hy5hqi0/clip_image00118_thumb1.gif?imgmax=800)
![clip_image001[22] clip_image001[22]](http://lh4.ggpht.com/_MLcxcpYx4ws/SwzWl6OUg3I/AAAAAAAAANQ/RcilPB2mIPA/clip_image00122_thumb2.gif?imgmax=800)
![clip_image001[28] clip_image001[28]](http://lh5.ggpht.com/_MLcxcpYx4ws/SwzWusmmELI/AAAAAAAAANY/wUS_zW6ki9w/clip_image00128_thumb1.gif?imgmax=800)

![clip_image001[5] clip_image001[5]](http://lh3.ggpht.com/_MLcxcpYx4ws/SwzM_RDtADI/AAAAAAAAAK8/zkr9vP4q2vs/clip_image0015_thumb1.gif?imgmax=800)
![clip_image001[7] clip_image001[7]](http://lh4.ggpht.com/_MLcxcpYx4ws/SwzOAnQRJPI/AAAAAAAAALk/vb2oOEnMBUs/clip_image0017_thumb.gif?imgmax=800)
![clip_image001[17] clip_image001[17]](http://lh4.ggpht.com/_MLcxcpYx4ws/SwzOLCxnHiI/AAAAAAAAALs/3fkkIZzFJT0/clip_image00117_thumb.gif?imgmax=800)
![clip_image001[19] clip_image001[19]](http://lh6.ggpht.com/_MLcxcpYx4ws/SwzOSqhni5I/AAAAAAAAAL0/nBSt4EAoHHg/clip_image00119_thumb.gif?imgmax=800)
![clip_image001[21] clip_image001[21]](http://lh5.ggpht.com/_MLcxcpYx4ws/SwzTsqvW07I/AAAAAAAAAL8/FFBYC3GrvRk/clip_image00121_thumb.gif?imgmax=800)
![clip_image001[5] clip_image001[5]](http://lh5.ggpht.com/_MLcxcpYx4ws/SwzT3_MVOSI/AAAAAAAAAME/wNMchPflnTM/clip_image0015_thumb2.gif?imgmax=800)
![clip_image001[25] clip_image001[25]](http://lh6.ggpht.com/_MLcxcpYx4ws/SwzUAm7rjtI/AAAAAAAAAMM/sYtquuJ587M/clip_image00125_thumb1.gif?imgmax=800)