What is the y-intercept?

We have seen in a previous post the gradient of a straight line graph. Today we are going so have a look at the y-intercept.

Now as you know a graph is composed of two axes. The y-axis and the x-axis as shown in fig 1.

Fig 1

Now in order to find the y-intercept you will need a straight line that passes through the y-axis, i.e it intercept the y-axis,  as seen in fig 2 below.

Fig 2

As you can see in fig 2 above all three lines crosses the y-axis. As a result the three lines would have a y-intercept.

How to obtain the y-intercept of a straight line?

1. If the x-axis starts at 0

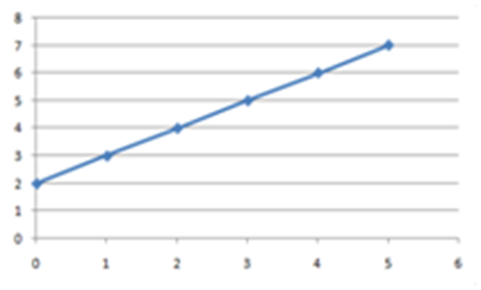
As you can see in fig 3 below the point at which the line crosses the y-axis is at the y=2 coordinate. Hence the y-intercept is 2.

We can thus define the y-intercept as being the value of the y-coordinate when the x-coordinate is 0. 

Fig 3

2. If the x-axis does not start at 0

As you can see in fig 4 below the x-axis does not start at 0. Hence as you may have guess wrongly the y-intercept is not 2 since according to the definition the y-intercept is the y-coordinate when the x-coordinate is 0.

So how do you obtain the y coordinate.

Fig 4

You will first have to calculate the gradient of the line using the method described in this post.

The gradient in this case is 1.

You will use the equation y = mx + c  and a coordinate on the line in this case (3,2).

y = 2

x=2

gradient = m =1

Hence the only variable left is c, the y-intercept.

3 = 1*2 + c

c = 3 – 2 =1

The y-intercept of the line is thus 1.

You should thus be very careful to check that the x-axis starts with 0 or does not start with 0 so as to choose which of the two methods to use.