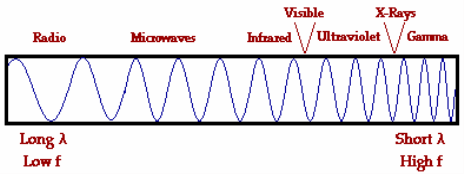
As we have seen in this post during a collision between two object the velocity of the two colliding objects changes. Hence you would agree that he kinetic energy of the objects would change.
We have also seen in this post that in all collisions the sum of linear momentum is a constant. This is the principle of conservation of linear momentum. However as we are going to see in some collisions, elastic collisions, the sum of kinetic energy is also constant. That is the sum of the kinetic energies of the objects before the collision is the same as the sum of the kinetic energies after the collision.
We are now going to see an example of how to use this “principle” which i am going to call the “principle of conservation of kinetic energy”.
Fig 1 below shows two objects travelling towards each other and fig 2 shows the two objects separating after the two objects have separated.
So if the principle of conservation of kinetic energy applies then it means that Sum of kinetic energy before collision = sum of kinetic energy after collision
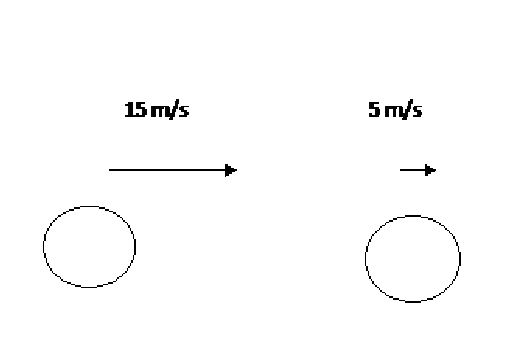
Fig 1 Before collision
Before the collision
Sum of kinetic energy before collision = kinetic energy of object 1 + kinetic energy of object 2
= 1/2m1u12 + 1/2m2v12
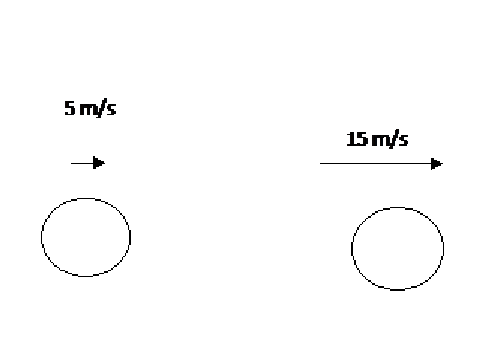
Fig 2 After collision
After the collision
Sum of kinetic energy after collision = kinetic energy of object 1 + kinetic energy of object 2
= 1/2m1u22 + 1/2m2v22
If you refer back to the principle then
Sum of kinetic energy before collision = sum of kinetic energy after collision
1/2m1u12 + 1/2m2v12 = 1/2m1u22 + 1/2m2v22
Example
Two balls of mass 1.0 kg are travelling towards each other at a speed of 5.0 m/s towards the right (ball 1) and 5.0 m/s towards the left (ball 2) respectively. If after separation one of them moves moves off a speed of 5 m/s towards the right (ball 2 ) calculate the speed of the other ball.
Sum of kinetic energy before collision = sum of kinetic energy after collision
1/2m1u12 + 1/2m2v12 = 1/2m1u22 + 1/2m2v22
1/2*1.0*5.02 + 1/2*1.0*(-5.0)2 = 1/2*1.0*u22 + 1/2*1.0*5.02
Solving for u2 the velocity of object 1 after the collision
12.5+ 12.5 = 0.5*u22+12.5
12.5= 0.5*u22
12.5 /0.5 = 25 =u22
u22 = 25
There can be two solution to u2
First u2=-5 m/s and secondly u2= 5 m/s
Since the second ball is already travelling towards the right and according to the principle of conservation of linear momentum then the only solution is
u2=-5 m/s


![clip_image001[6] clip_image001[6]](http://lh6.ggpht.com/_MLcxcpYx4ws/S4iykjrLRPI/AAAAAAAAAbU/YuNPHgeuh8o/clip_image001%5B6%5D_thumb%5B2%5D.gif?imgmax=800)
![clip_image001[5] clip_image001[5]](http://lh5.ggpht.com/_MLcxcpYx4ws/S4QNKq9OLdI/AAAAAAAAAa8/xgYZjdlOWQc/clip_image001%5B5%5D_thumb%5B1%5D.gif?imgmax=800)
![clip_image001[9] clip_image001[9]](http://lh3.ggpht.com/_MLcxcpYx4ws/S4QNced9pQI/AAAAAAAAAbE/jt6RVyMU5ow/clip_image001%5B9%5D_thumb%5B1%5D.gif?imgmax=800)

![clip_image001[5] clip_image001[5]](http://lh5.ggpht.com/_MLcxcpYx4ws/S3bgzfq962I/AAAAAAAAAZI/ZdT-y22DVW8/clip_image001%5B5%5D_thumb.gif?imgmax=800)

![clip_image001[6] clip_image001[6]](http://lh3.ggpht.com/_MLcxcpYx4ws/S3T0jaSRL9I/AAAAAAAAAYo/OWnvceOK82w/clip_image001%5B6%5D_thumb%5B1%5D.gif?imgmax=800)
![clip_image001[4] clip_image001[4]](http://lh4.ggpht.com/_MLcxcpYx4ws/S3LsfPW5EaI/AAAAAAAAAYc/2JpvtT1z9y4/clip_image0014_thumb1.gif?imgmax=800)

![clip_image001[4] clip_image001[4]](http://lh6.ggpht.com/_MLcxcpYx4ws/S21xqNgcOLI/AAAAAAAAAXI/XckrYkpGv7w/clip_image001%5B4%5D_thumb%5B2%5D.gif?imgmax=800)
![clip_image001[6] clip_image001[6]](http://lh5.ggpht.com/_MLcxcpYx4ws/S21x78cQCII/AAAAAAAAAXQ/IXoi1-oMlCQ/clip_image001%5B6%5D_thumb%5B2%5D.gif?imgmax=800)
![clip_image001[1] clip_image001[1]](http://lh3.ggpht.com/_MLcxcpYx4ws/S2bhE8udrwI/AAAAAAAAAWg/Gg0vUR8qQ6c/clip_image001%5B1%5D_thumb%5B1%5D.gif?imgmax=800)
![clip_image001[3] clip_image001[3]](http://lh3.ggpht.com/_MLcxcpYx4ws/S2bhLy85seI/AAAAAAAAAWo/n7lDvMU9jok/clip_image001%5B3%5D_thumb%5B1%5D.gif?imgmax=800)
![clip_image001[7] clip_image001[7]](http://lh3.ggpht.com/_MLcxcpYx4ws/S2bhUmuilEI/AAAAAAAAAWw/fyfvw0WU_lA/clip_image001%5B7%5D_thumb%5B1%5D.gif?imgmax=800)
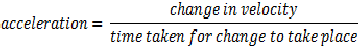
![clip_image002[1] clip_image002[1]](http://lh6.ggpht.com/_MLcxcpYx4ws/S2bhb-gM9qI/AAAAAAAAAW4/uKK6ytnVc-w/clip_image002%5B1%5D_thumb%5B1%5D.gif?imgmax=800)