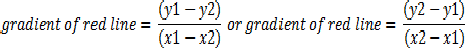The gradient of a line or the slope of a line is an indication of how steep a line is at a particular point. The gradient is particularly important in Physics and as a result it is particularly important that you understand how to calculate it perfectly.
Gradient of a straight line
We have in fig 1 below two straight lines that have different slopes. We are going to see how to determine the gradient of both straight lines.
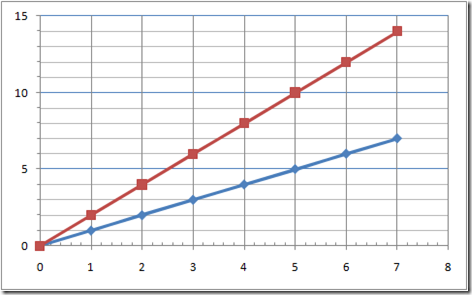
As you can see, there are two straight lines: a blue one and a red one.
It is clear that the red one is steeper than the blue one and as a result its slope would be greater. Consequently the gradient of the red line is greater than that of the blue line.
But do you know how to determine the gradient of the two straight lines mathematically?
Let us look at the red line first and then you are going to look at the blue line.
Loot at the line and the take two coordinated off the line.
I have taken (1,2) and (4,8)
These two coordinates would be considered as (x1,y1) and (x2,y2) such that
From the first coordinate you have x1 =1 and y1=2
from the second coordinate you have x2 =4 and y2 = 8
In order to calculate the gradient of the red line we are going to use the equation below
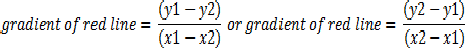
Hence using the equation above the gradient of the red line is calculated as shown
gradient of red line = (8-2)/(4-1) =6/3 = 2
If you want to check if you can calculate the gradient of the blue line you can do so by repeating the process above.
What you would also find is that any pair of coordinates that you take will give you the same gradient. Which mean that at any point along the straight line the gradient is the same.
Gradient of a curve
The method to calculate the gradient at a point along a curve is slightly different. In that you first have to draw a tangent to the curve at the point that you want to calculate the gradient.
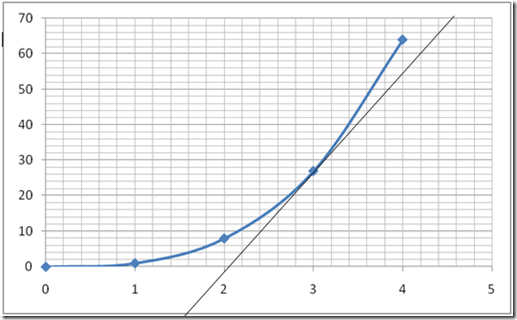
Fig 2
As you can see in fig 2 above, I want to calculate the gradient of the curve at the point (3, 27) as a result I have drawn a tangent to the curve at that point. If you do not know how to draw a gradient I can show you later on in a later post.
Now that you have drawn a tangent at the point that we want (3,27) you will need to choose any two coordinates on the tangent line.
I have chosen (2.5 , 4) and (4 , 60). You can choose any coordinate on the tangent.
Hence using the coordinated below the gradient of the curve at the point (3,27) is
Gradient of curve at point (3,27) = (60 – 4)/(4 - 2.5)= 56/1.5 = 37.3 =37 (2 sf)
As you can see it is easy to calculate the gradient of a straight line or a curve at a particular point.


![clip_image001[13] clip_image001[13]](http://lh5.ggpht.com/_MLcxcpYx4ws/S2HQVQii5dI/AAAAAAAAAVM/kYuexTziG8I/clip_image001%5B13%5D_thumb%5B1%5D.gif?imgmax=800)
![clip_image001[11] clip_image001[11]](http://lh4.ggpht.com/_MLcxcpYx4ws/S2HQeGZq73I/AAAAAAAAAVU/7IfK_8z9LCE/clip_image001%5B11%5D_thumb%5B1%5D.gif?imgmax=800)



![clip_image001[6] clip_image001[6]](http://lh6.ggpht.com/_MLcxcpYx4ws/S16GKPPrySI/AAAAAAAAAUI/FxSgozbqkrM/clip_image0016_thumb3.gif?imgmax=800)
![clip_image001[8] clip_image001[8]](http://lh6.ggpht.com/_MLcxcpYx4ws/S16GS8FM7pI/AAAAAAAAAUM/nux0eTDx81g/clip_image0018_thumb2.gif?imgmax=800) Fig 3
Fig 3![clip_image001[5] clip_image001[5]](http://lh3.ggpht.com/_MLcxcpYx4ws/S16GspHqWbI/AAAAAAAAAUU/HSmLAmI-aAY/clip_image0015_thumb2.gif?imgmax=800)
![clip_image001[3] clip_image001[3]](http://lh5.ggpht.com/_MLcxcpYx4ws/S16G-GGSw6I/AAAAAAAAAUc/d-KYTy2K7ao/clip_image0013_thumb2.gif?imgmax=800)
![clip_image001[11] clip_image001[11]](http://lh5.ggpht.com/_MLcxcpYx4ws/S16HSyHPFXI/AAAAAAAAAUk/xAcPRiSqd1c/clip_image00111_thumb1.gif?imgmax=800)
![clip_image001[13] clip_image001[13]](http://lh3.ggpht.com/_MLcxcpYx4ws/S16HjTz7zKI/AAAAAAAAAUs/06DMGVFvG14/clip_image00113_thumb2.gif?imgmax=800)
![clip_image002[4] clip_image002[4]](http://lh4.ggpht.com/_MLcxcpYx4ws/S1m0GM7yTsI/AAAAAAAAATw/rckfmhJMAPA/clip_image0024_thumb1.gif?imgmax=800)
![clip_image002[6] clip_image002[6]](http://lh6.ggpht.com/_MLcxcpYx4ws/S1m0Ybn_EJI/AAAAAAAAAT4/guHsnzOPvRY/clip_image0026_thumb3.gif?imgmax=800)
![clip_image002[7] clip_image002[7]](http://lh4.ggpht.com/_MLcxcpYx4ws/S1bTOinr_6I/AAAAAAAAATY/5k4AVjWK0ek/clip_image002%5B7%5D_thumb%5B1%5D.gif?imgmax=800)
![clip_image002[5] clip_image002[5]](http://lh6.ggpht.com/_MLcxcpYx4ws/S1WS0Hv8B0I/AAAAAAAAAS4/GGGFU7HTLjU/clip_image0025_thumb1.gif?imgmax=800)